ベイズの時代
～現場主義への回帰として～

ネットワーキング事業部の森といいます。私は入社以来30年以上ネットワーク関連の業務に携わってきました。本日はちょっと趣向を変えてデータ分析について思うことを書いてみます。

21世紀の幕開けとなる2001年、マイクロソフト社のビル・ゲイツ氏は「21世紀はベイズの時代である」と述べました。ベイズという名前はベイズ理論、ベイズ統計、ベイズ推定、ベイジアンネットワークなど、確率論、統計学、そしてデータ分析の話題ではいたるところに登場します。さて、ベイズとはどういう人だったのでしょうか。

トーマス・ベイズは現代を代表する数学者なのかと思いきや、18世紀初めころの英国の牧師さんです。牧師の仕事のかたわら保険の掛け金の計算などを行っていたようです。保険の設計には高度な確率計算が要求されることからそんな地道な計算作業の中でこの新たな確率論、ベイズ理論に至ったのではないかと想像しています。

ではベイズ理論とはどういう理論なのでしょうか。よく次のような式が登場します。

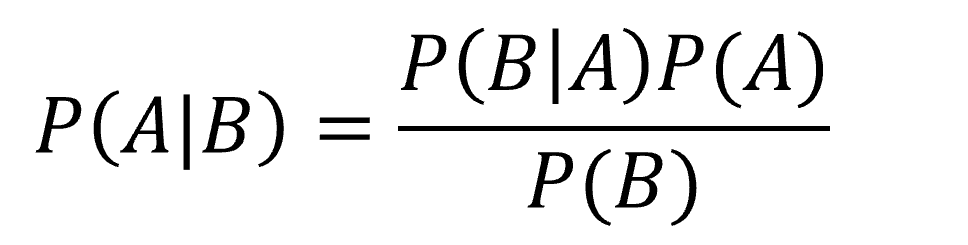
これの詳細な解説は他の書籍に譲ることとして、これを感覚的に理解するためにこんな問題は如何でしょうか。

さて、これにどういうアプローチをしますか。従来からの確率論だと釣り上げる1匹の魚が鯉である確率を求め、それから期待値を求めるという手法をとります。ある1匹が鯉である確率というのは全国あるいはその地域の魚の種類ごとの分布、その池とその流域の生態系、環境条件などをつぶさに調査して計算するという手法になると思われます。これを事前確率といいますが、それを求めるのは大変な作業です。これまでの確率論はこうした確率というものがしっかりと定義されその数値も明確であることを前提としています。サイコロの目のように確率がある確定値をとると想定される時には有効ですが、このような場面ではあまり有効とは思われません。それで結局、何匹なの？と問われると答えは、わからない、ということになるでしょう。

それでは次の問題は如何でしょうか。

実際に1匹釣り上げて確かめる、という行為が入ったことでちょっとムードが変わりました。どうして釣り上げた1匹が鯉だったのかを分析することで、この池にはどんな魚がどのくらいいるのかが見えてくるということです。これを事前確率に対して事後確率といいます。それまでの確率の理論が原因を事前確率として確定した前提で結果を導くアプローチだったのに対して、ベイズ理論は結果からスタートして原因そのものを事後確率として分析していく、というものです。そして、2匹目、3匹目という経験を加えていくことで分析の精度を継続的に向上できることもその大きな特長です。

現代のビジネスの現場においては、サイコロのようなものを振るというよりも、鯉の問題が示すように何が潜んでいるか分からないようなところで一つ一つ地道にデータを積み上げてチャンスを探すという場面の方が多いです。データ分析は感染症拡大状況の分析でも登場していますが、ある事象が発生する原因とメカニズムを厳密に解明するよりも、現場から具体的なデータを採取するところから着手して実際に何が起きているのか、そして原因として潜む事象とその確率を探ります。こうした時代の要請にベイズ理論がぴったりとはまったのだと思います。

私は、ビジネスの視線からみてベイズ理論は現場中心主義であり、そういう意味で現場回帰のアプローチであると捉えています。上記の鯉の問題の例で対象としているのは全国や地域のあらゆる種類の魚の分布のような遠大なものではなく、あくまで「この池にいる魚」です。その場所を理解して何らかの効果を得るための第一歩は、他でもないその場所に深い愛着と関心を持ってデータを調べ始めることです。まさに百聞は1データに如かず、です。

当社のIoT-Edgeネットワーク事業がめざすものも同じです。現場に備え付けたセンサーからのデータをネットワークを介して吸い上げるところから始まり、データ分析との組み合わせによって現場で起きていることの根源そして真の意味を探ることで品質改善、生産性向上を図るものです。当社は、お客さまとその現場に長い間お付き合いさせていただいてまいりました。その長く貴重な経験から得ることができた「現場を見て、現場目線で考え、常に現場に寄り添う」という現場力がそのための大きな力になるのではと考えています。

ちなみに、問題2の解答はベイズ理論によれば「5.5匹」です。計算方法に興味のある方は個別にお問い合わせください。